Оптические параметры
Показатель преломления
Показателем преломления 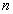 называется отношение скорости света в вакууме к скорости света в
материале.
называется отношение скорости света в вакууме к скорости света в
материале. 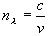 В каталоге показатель преломления рассчитывается по дисперсионным формулам.
В каталоге показатель преломления рассчитывается по дисперсионным формулам.
Дисперсия
Зависимость показателя преломления от длины волны называется дисперсией
показателя преломления 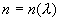 .
Численно дисперсия характеризуется несколькими величинами. .
Численно дисперсия характеризуется несколькими величинами.
Основной коэффициент дисперсии (число Аббе) - 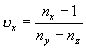 ,
где ,
где 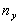 и
и 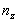 -
показатели преломления для длин волн, ограничивающих какой-либо
диапазон спектра, а -
показатели преломления для длин волн, ограничивающих какой-либо
диапазон спектра, а 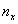 -
показатель преломления для длины волны, расположенной внутри диапазона. -
показатель преломления для длины волны, расположенной внутри диапазона.
Основная средняя дисперсия определяется выражением 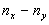 ,
где ,
где 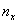 и и
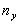 показатели
преломления для длин волн, ограничивающих некоторую часть спектра. показатели
преломления для длин волн, ограничивающих некоторую часть спектра.
Относительная частная дисперсия это отношение основных средних
дисперсий для разных частей спектра. Характеризует степень изменения
дисперсионных свойств вещества по спектру. 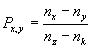 ,
где ,
где 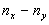 и
и 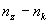 основные
средние дисперсии для частей спектра ограниченных соответственно
длинами волн x, y и z, k. основные
средние дисперсии для частей спектра ограниченных соответственно
длинами волн x, y и z, k.
Все дисперсионные характеристики рассчитываются по дисперсионным формулам.
Коэффициент пропускания
Спектральным внутренним коэффициентом пропускания (коэффициент
пропускания) называется отношение светового потока, прошедшего
через материал, к падающему потоку 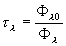 . .
Падающий поток должен быть монохроматическим, параллельным и направленным
перпендикулярно к плоскопараллельной пластинке изотропного, однородного,
не люминесцентного, не фотохромного материала.
Цветовой код
Цветовой код описывает границу пропускания стекла в видимой
части спектра. Эта характеристика задаёт две длины волны 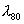 и
и 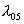 ,
на которых коэффициент пропускания составляет 0.8 и 0.05 соответственно. ,
на которых коэффициент пропускания составляет 0.8 и 0.05 соответственно.
Показатель ослабления
Показатель ослабления - это величина, обратная расстоянию,
на котором поток излучения ослабляется в результате поглощения и
рассеивания в стекле в 10 (или e) раз. 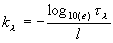 ,
где ,
где 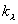 - показатель ослабления,
- показатель ослабления, 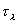 - коэффициент пропускания,
- коэффициент пропускания, 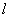 - толщина слоя материала.
- толщина слоя материала.
Механические параметры
Плотность
Плотностью 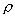 называется масса единицы объёма
называется масса единицы объёма 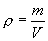 . .
Коэффициент Пуассона
Коэффициент Пуассона 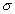 (коэффициент
поперечной деформации) - отношение относительного поперечного
сужения (расширения) (коэффициент
поперечной деформации) - отношение относительного поперечного
сужения (расширения) 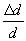 к относительному продольному удлинению (сжатию)
к относительному продольному удлинению (сжатию) 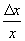 ,
т. е. ,
т. е. 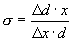 . .
Для аморфных тел коэффициент Пуассона одинаков во всех направлениях,
для кристаллических - зависит от направления приложенной силы.
Модуль Юнга
Модуль Юнга 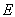 определяется как отношение напряжения к внутренней деформации, т.
е.
определяется как отношение напряжения к внутренней деформации, т.
е. 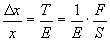 ,
где ,
где 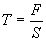 - сила на единицу площади, перпендикулярно которой она приложена.
- сила на единицу площади, перпендикулярно которой она приложена.
Для аморфных тел модуль Юнга одинаков во всех направлениях, однако
в случае кристаллов значение 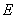 зависит от направления, в котором приложена сила.
зависит от направления, в котором приложена сила.
Модуль сдвига
Модуль сдвига связывает модуль Юнга и коэффициент Пуассона
по следующей формуле:
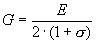 . .
Истираемость
Под истираемостью понимается относительная твердость 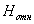 по сошлифовыванию, которая определяется как отношение объема сошлифованного
свободным абразивом эталонного стекла к объему стекла тестируемого
стекла, сошлифованному в тех же условиях.
по сошлифовыванию, которая определяется как отношение объема сошлифованного
свободным абразивом эталонного стекла к объему стекла тестируемого
стекла, сошлифованному в тех же условиях.
Значение 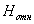 служит также технологическим критерием скорости износа стекла при
шлифовании.
служит также технологическим критерием скорости износа стекла при
шлифовании.
Для каждого каталога эта величина определяется по-своему.
Оптический
коэффициент напряжения
Оптический коэффициент напряжения определяет разность оптического
хода поляризованных лучей в стекле и характеризует двойное лучепреломление,
возникающее при напряжении.
При возникновении упругих деформаций в стекле проявляются фотоупругие
свойства. Стекло становится веществом анизотропным, что приводит
к появлению двойного лучепреломления: луч света, проходящий через
стекло, поляризуется и разлагается на два луча - обыкновенный и
необыкновенный, плоскости поляризации которых взаимно перпендикулярны.
Это явление, специфичное для прозрачных материалов, называют фотоупругостью.
Показатели преломления стекла для поляризованных лучей отличаются
от показателей преломления стекла в ненапряженном состоянии. Фотоупругость
стекла характеризуется фотоупругими постоянными 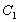 и
и 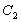 ,
выражающими приращение значения показателя преломления стекла для
лучей света, поляризованных в направлениях, параллельном и перпендикулярном
действию напряжения, а также оптическим коэффициентом напряжения ,
выражающими приращение значения показателя преломления стекла для
лучей света, поляризованных в направлениях, параллельном и перпендикулярном
действию напряжения, а также оптическим коэффициентом напряжения
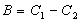 . .
После снятия напряжения стекло становится изотропным материалом.
Твёрдость
Твердость является мерой сопротивления остаточной деформации
или разрушению.
Существует несколько методов определения твердости. Наиболее распространенный
метод определения твердости заключается в измерении сопротивления
изучаемого материала проникновению шарика или пуансона (индентора)
установленной формы из соответствующего материала. Величина твердости
определяется усилием, приложенным к единице площади поверхности
в месте контакта пуансона (индентора) с исследуемым веществом и
имеет размерность 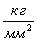 (твердость по Кнупу, Бринеллю, Викерсу). Стандартом на определение
твёрдости по Кнупу является документ ISO 9385.
(твердость по Кнупу, Бринеллю, Викерсу). Стандартом на определение
твёрдости по Кнупу является документ ISO 9385.
При другом определении твердости используется способность вещества
подвергаться царапанью другим веществом. Классификация ведётся в
цифровой шкале от 1 до 10, причем эти две цифры соответствуют твердости
талька и твердости алмаза. Эти числа определяют твердость по
Моосу.
Химические характеристики
Химические характеристики российского ГОСТ
В российском ГОСТ установлено два показателя химической устойчивости
стекла: устойчивость полированной поверхности детали к воздействию
влажной атмосферы (климатическая устойчивость) без конденсации
паров (~75 % относительной влажности) и устойчивость к действию
пятнающих агентов (пятнаемость) - нейтральной воде, слабокислым
и щелочным водным растворам.
По устойчивости к действию влажной атмосферы силикатные оптические
стекла делятся на группы:
А - неналётоопасные,
Б - промежуточные,
В - налетоопасные.
Большинство оптических стекол относятся к группе А. Оптические
детали из налетоопасных стекол сразу же после обработки покрывают
защитными пленками.
По устойчивости к действию пятнающих агентов оптические стекла
делят на следующие группы:
I - непятнающиеся,
II - средней пятнаемости,
III - пятнающиеся,
IV - нестойкие стекла, требующие обязательного применения защитных
покрытий.
Климатическая устойчивость
Климатическая устойчивость - это степень влияния на стекло
водных паров атмосферы. Это влияние, особенно при высокий температурах,
приводит к появлению мутной плёнки на поверхности материала. Химическая
реакция возникает в результате реакции нейтральной воды, содержащейся
в атмосфере co стеклом.
Техническая информация о способах определения климатической устойчивости
для каталога O'Hara доступна по адресу http://www.ohara-gmbh.com/e/katalog/tinfo_4_2.html.
В каталоге Schott 2000 климатическая устойчивость определяется
в результате изучения изменения коэффициента пропускания образца
после выдерживания его в течение 30 часов при температуре от 40
до 50 C. Классификация производится по приведённой таблице.
| Группа устойчивости |
1 |
2 |
3 |
4 |
| Изменение коэф. пропускания |
< 0,3% |
>= 0,3%
< 1% |
>= 1%
< 2% |
>= 2% |
Устойчивость к кислоте
В результате взаимодействия кислотной среды с поверхностью стекла
на стекле образуются пятна и области с разрушенным поверхностным
слоем. Кислотная устойчивость определяет степень влияния
кислотной среды на стекло.
Группы кислотной устойчивости для каталогов O'Hara и Schott 2000
определяются по ISO 8424.
Устойчивость к щёлочи
Устойчивость к щёлочи определяет степень влияния щелочных
растворов на стекло.
Стандартный метод определения устойчивости к щёлочи описывается
в документе ISO 10629.
В каталоге Schott 2000 группы устойчивости к щёлочи определяются
по времени, необходимому для удаления слоя 0.1 мм щёлочной средой
при температуре 50 C. Распределение по группам приведено в таблице.
| Группа |
1 |
2 |
3 |
4 |
| Время, часы |
> 4 |
1 - 4 |
0.25 - 1 |
< 0.25 |
Фосфатная устойчивость
Водные растворы, используемые для очистки оптических стёкол, обычно
содержат примеси, в том числе и полифосфаты. Фосфатная устойчивость
позволяет определить устойчивость оптических стёкол к таким жидкостям.
Группы фосфатной устойчивости для каталогов O'Hara и Schott 2000
определяются по ISO 9689.
Пятнаемость
В результате воздействий на поверхность стекла слабо кислотных
растворов (дыхание, испарина) происходит процесс "вымывания" некоторых
веществ, приводящий к образованию интерференционных цветных пятен
на поверхности. Устойчивость стекла к такого рода влияниям характеризуется
пятнаемостью.
В каталоге Schott 2000 группы по пятнаемости определяются
следующим образом:
Плоский полированный образец помещается в тестовую кювету сферической
формы с максимальным углублением 0.25 мм, на дне которой находится
несколько капель стандартного ацитата (pH=4.6) (I) или ацитата натрия
(pH=5.6) (II). Критерием принадлежности стекла к соответствующей
группе является время появления первого буро-синего пятна на поверхности
при температуре 25 C.
Группы классифицируются в соответствии с таблицей.
| Группа |
0 |
1 |
2 |
3 |
4 |
5 |
| Раствор |
I |
I |
I |
I |
II |
II |
| Время, часы |
100 |
100 |
6 |
1 |
1 |
0.2 |
| Изменение цвета |
нет |
да |
да |
да |
да |
да |
Температурные характеристики
Температурное изменение показателя
преломления
Показатель преломления зависит не только от длины волны излучения,
но также и от температуры.
Отношение изменения показателя преломления к изменению температуры
называется температурным коэффициентом показателя преломления.
Он может принимать как положительные, так и отрицательные значения.
Относительный температурный коэффициент показателя преломления 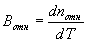 измеряется при определённом давлении воздуха, абсолютный
измеряется при определённом давлении воздуха, абсолютный 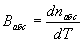 - в вакууме.
- в вакууме.
Температурный коэффициент линейного расширения
Международный стандарт: ISO 7991.
Температурный коэффициент линейного расширения (ТКЛР) 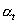 характеризует относительное удлинение
характеризует относительное удлинение 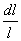 образца стекла при нагревании его на 1 градус:
образца стекла при нагревании его на 1 градус: 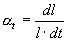 .
Значение ТКЛР изменяется в зависимости от диапазона температуры,
в котором он измеряется. .
Значение ТКЛР изменяется в зависимости от диапазона температуры,
в котором он измеряется. Что такое дисперционная формула
Дисперсионная формула - это аппроксимация, позволяющая
описывать зависимость показателя преломления от длины волны 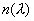 в
функциональном виде. в
функциональном виде.
Для каждой оптической среды определяется некоторый набор коэффициентов
(различный для разных формул), значения которых позволяют восстанавливать
показатель преломления в любой точке части спектра, где производилась
аппроксимация. Длины волн, ограничивающих эту часть спектра, должны
быть указаны для каждого отдельного разложения.
Описание дисперсионных формул
Формула Герцбергера (The Herzberger formula)
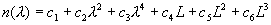 ,
где ,
где 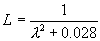
Формула Зелмейера (The Sellmeier formula)
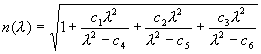
Формула Конради (The Conrady formula)
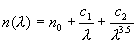
Формула Шотта (The Schott formula)
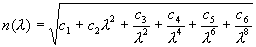
Формула Резника
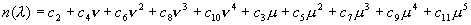 ,где ,где
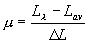 , , 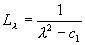 , , 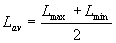 , , 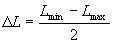 , , 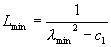 , , 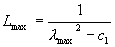 , ,
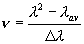 ,
, 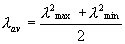 , , 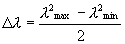 |